Introduction
Now you’re a pro with DFS and BFS. Let’s try using our search algorithms on a real problem.
For this project, you’ll need to use a data structure that’s similar (but not identical) to a binary tree - graphs. For a good introduction on what graphs are, reference Khan Academy’s “Describing Graphs”.
Given enough turns, a knight on a standard 8x8 chess board can move from any square to any other square. Its basic move is two steps forward and one step to the side or one step forward and two steps to the side. It can face any direction.
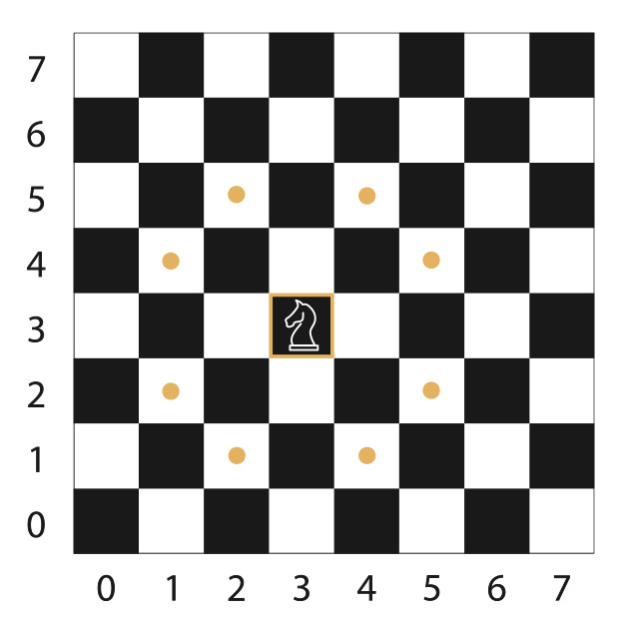
All the possible places you can end up after one move look like this:
In this problem, the chessboard can be represented as a graph:
Each square on the board is a node (or vertex). A knight’s valid moves from any square represent the edges (or connections) between the vertices. Thus, the problem of finding the shortest path for the knight’s movement becomes a graph traversal problem. The goal is to traverse the graph (the chessboard) to find the shortest route between two nodes (the start and end positions).
Vertices and Edges
The vertices in this graph are each of the possible positions on the chessboard, represented by a pair of coordinates like [x, y], where x and y are between 0 and 7.
The edges are the valid knight moves between vertices. For example, from [0,0], a knight can move to [2,1], [1,2], and so on. Each of these moves represents a connection between the vertex [0,0] and the other reachable vertices.
Graph Representation
While solving this problem, you don’t need to explicitly create a graph object with vertices and edges. Instead, you can think of the graph as implicit. The knight starts on a specific vertex, and the algorithm will dynamically explore all possible moves (edges) to other vertices (positions on the board) as it traverses the board.
Assignment
Your task is to build a function knight_moves that shows the shortest possible way to get from one square to another by outputting all squares the knight will stop on along the way.
You can think of the board as having 2-dimensional coordinates. Your function would therefore look like:
knight_moves([0,0],[1,2]) == [[0,0],[1,2]]
Sometimes there is more than one fastest path. Examples of this are shown below. Any answer is correct as long as it follows the rules and gives the shortest possible path.
knight_moves([0,0],[3,3]) == [[0,0],[2,1],[3,3]]orknight_moves([0,0],[3,3]) == [[0,0],[1,2],[3,3]]knight_moves([3,3],[0,0]) == [[3,3],[2,1],[0,0]]orknight_moves([3,3],[0,0]) == [[3,3],[1,2],[0,0]]knight_moves([0,0],[7,7]) == [[0,0],[2,1],[4,2],[6,3],[4,4],[6,5],[7,7]]orknight_moves([0,0],[7,7]) == [[0,0],[2,1],[4,2],[6,3],[7,5],[5,6],[7,7]]
- Think about the rules of the board and knight, make sure to follow them.
- For every square there is a number of possible moves, choose a data structure that will allow you to work with them. Don’t allow any moves to go off the board.
- Decide which search algorithm is best to use for this case. Hint: one of them could be a potentially infinite series.
- Use the chosen search algorithm to find the shortest path between the starting square (or node) and the ending square. Output what that full path looks like, e.g.:
> knight_moves([3,3],[4,3])
=> You made it in 3 moves! Here's your path:
[3,3]
[4,5]
[2,4]
[4,3]